Sistemas de numeración

Un sistema de numeración es un conjunto de reglas y convenciones utilizadas para representar cantidades numéricas mediante símbolos.

• El sistema decimal es un sistema de numeración que utiliza diez símbolos diferentes para representar cantidades numéricas: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9.

• El sistema binario es un sistema de numeración que utiliza dos símbolos diferentes para representar cantidades numéricas: 0, 1

• El sistema octal es un sistema de numeración que utiliza ocho símbolos diferentes para representar cantidades numéricas: 0, 1, 2, 3, 4, 5, 6, 7

• El sistema hexadecimal es un sistema de numeración que utiliza dieciséis símbolos diferentes para representar cantidades numéricas: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C ,D, E y F

Tabla de los 17 primeros números

HEX	DEC	OCT	BIN
0	0	0	0
1	1	1	1
2	2	2	10
3	3	3	11
4	4	4	100
5	5	5	101
6	6	6	110
7	7	7	111
8	8	10	1000
9	9	11	1001
A	10	12	1010
B	11	13	1011
C	12	14	1100
D	13	15	1101
E	14	16	1110
F	15	17	1111
10	16	20	10000

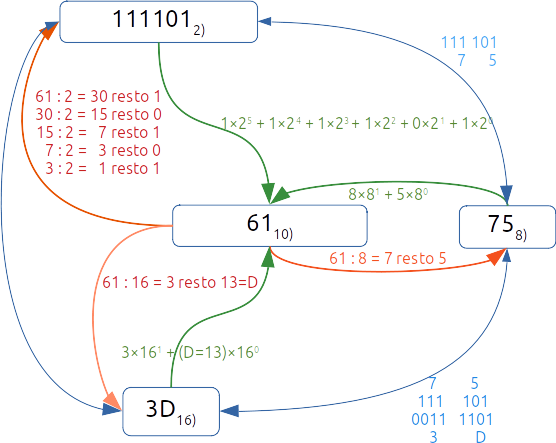
Conversión de base N a decimal

(Teorema fundamental de la numeración)

\begin{eqnarray} TFM: N_{10} = \sum_{i=m}^{n}(digito)base^i \end{eqnarray}

Ejemplo:

\[ \begin{align}\begin{aligned}111101_{2)} &= 1×2^5 + 1×2^4 + 1×2^3 + 1×2^2 + 0×2^1 + 1×2^0 = 61_{10)}\\75_{8)} &= 7×8^{1} + 5×8^{0} = 61_{10)}\\331_{4)} &= 3×4^2 + 3×4^1 + 1×4^0 = 61_{10)}\\3D_{16)} &= 3×16^1 + (D=13)×16^0 = 61_{10)}\end{aligned}\end{align} \]

Base decimal a base N

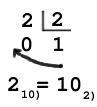
Ejemplo de base decimal a base binaria 61 _{10) → 2)}

Ejemplo de base decimal a base octal 61 _{10) → 8)}

\[ \begin{align}\begin{aligned}61 : 8 &= 7\ resto \textbf{5}\\7 : 8 &= 0\ resto\ \textbf{7}\\61_{10)} &= 75_{8)}\end{aligned}\end{align} \]

Ejemplo de base decimal a base hexadecimal 61 _{10) → 16)}

\[ \begin{align}\begin{aligned}61 : 16 &= 3\ resto\ (13=\textbf{D})\\3 : 16 &= 0 \ resto\ \textbf{3}\\61_{10)} &= 3D_{8)}\end{aligned}\end{align} \]

Base N a base M ≠ N ≠ 10

1. (TFM) pasamos a base M → base 10

2. De base 10 a base N

Ejemplo: Como se escribiría 3D ₁₆₎ en base 8

\[ \begin{align}\begin{aligned}3D_{16)} &= 3×16^1 + (D=13)×16^0 = 61_{10)}\\61 : 8 &= 7\ resto\ \textbf{5}\\7 : 8 &= 0 \ resto\ \textbf{7}\\61_{10)} &= 75_{8)}\end{aligned}\end{align} \]

Ejemplo: Como se escribiría 21 ₁₂₎ en base 5

Primero pasamos a base 10:

\[21_{12)} = 2 \times 12^{1} + 1 \times 12^0 = 25_{10)}\]

y de base 10 pasamos a base 5:

\[ \begin{align}\begin{aligned}25 : 5 &= 5\ resto\ \textbf{0}\\5 : 5 &= 1\ resto\ \textbf{0}\\1 : 5 &= 0\ resto\ \textbf{1}\\25_{10)} &= 100_{5)}\end{aligned}\end{align} \]

finalmente queda:

\[21_{12)} = 100_{5)}\]

Ejemplo: Como se escribe 2A ₁₅₎ en base 3

Primero base 10

\[2A_{15)} = 2 \times 15^1+A \times 15^0 = 30 + A = 30 + 10 = 40_{10)} =\]

y de base 10 pasamos a base 3:

\[ \begin{align}\begin{aligned}40 : 3 &= 13\ resto\ \textbf{1}\\13 : 3 &= 4\ resto\ \textbf{1}\\4 : 3 &= 1\ resto\ \textbf{1}\\1 : 3 &= 0\ resto\ \textbf{1}\end{aligned}\end{align} \]

Finalemte queda:

\[2A_{15)} = 40_{10)} = 1111_{3)}\]

Cambio de base por agrupaciones (binaria, octal, hexadecimal)

Para el caso de la base 2,8 y 16, podemos hacer agrupaciones 8 → (3,3) y en 16 → (4,4)

Ejemplo 1000 ₁₀₎ = 0011 1110 1000 ₂₎

0011 1110 1000

HEX: 3 E 8

001 111 101 000

OCT : 1 7 5 0

Queda:

3E8 ₁₆₎ = 0011 1110 1000 ₂₎ = 1750 ₈₎ = 1000 ₁₀₎

Resumen